<2022-Jhanani-Min-Max Q-learning for multi-player persuit-evasion games>

Abstract

• 目标：考虑steering an evader到达目的地的同时，避免被multiple pursuers捕获。

• 难点：high-dimensional and computationally intractable problem

• 方法：

  1. 首先将多智能体追逃博弈问题，formulate为一系列的离散矩阵游戏
  2. 为了简化求解过程，将high-dimensional state space转化为low-dimensional manifold，并且将连续的action space转化为featured-based space（即原始空间的discrete abstraction）
  3. 在变换以后的状态、动作空间的基础上，随后采用min-max Q-learning，来生成entries of the payoff matrix of the game，随后获得了evader在各个阶段的最优动作
  4. 最后，进行广泛的数值模拟，评估策略的性能，包括evader在不被捕获的情况下，到达所需目标位置的能力，以及计算效率

1. Introduction

在dynamic non-zero-sum multi-player game中可以研究agent之间的不确定交互，这类问题中特殊的一种就是多智能体的追逃博弈问题（pursuit-evasion games，PEGs）。

在本文中，考虑将evader引导至目标位置，同时避免被multiple pursuers捕获。该问题具有高维特征，所以要找到精确的解决方案是一项复杂的任务。

尤其是，PEG的状态空间由高维向量组成，这些向量与所有agents的速度、位置向量串联。类似的，所有agents的组合行动空间也是高维的。

• 在本文中，state space、action space都是==连续的==，要获得精确解非常困难，所以在实践中首选==近似解==
• min-max Q-learning + function approximation：来获得Q-function的近似（Q-function可以表征逃避者对任何状态下的不同玩家所采取的行动的reward）
• 为了独立讨论特定参数在训练过程中的影响，特别是agents的数量和速度，在low-dimensional manifold中进行训练（通过对连续的state space做非线性变换、对连续的action space（feature-based action space）做离散抽象得到）
• agents的交互：通过不同条件下的捕获时间来描述==（？）==

• 离散的actions：对应于不同agents的意图==（？）==

• 近似的Q-function用来构建描述每个阶段==two-player game==的matrix，matrix的解就是evader在每个阶段的policy

• pursuers可以采用后一轮博弈引发的策略，也可以采用类似于relay pursuit的predetermined policy（即只有距离evader最近的pursuer才会试图捕获）

Contributions

1. propose a systematic way：将多智能体动态非零和博弈，简化为一系列的two-player静态零和博弈，每个博弈都可以表示为线性过程（每个静态博弈的收益，决定了evader在该阶段的动作，反过来又决定了evader policy的表现）
2. 构建收益时考虑了：
   1. evader被捕获的风险指标
   2. evader到达目标位置的所需时间
3. 采用min-max Q-learning来确定博弈过程中，每个阶段的entried of payoff matrix
4. 原始高维状态，转换到了低维流型中，低维空间中使用捕获时间作为参数，而不是position and velocity（所以新的状态空间，对于agents数量 or agents的动态模型，是不变的），这是一个==关键属性==
5. 将连续的动作空间与feature-based动作空间关联，feature-based动作空间，是一个只有少量动作的离散空间，这些动作会影响一个 or 多个agent的捕获时间/目标时间，离散动作允许evader根据环境的需要在不同的空间方向上移动。

2. Preliminaries and problem formulation

2.2 Equation of Motion

$$\dot{\boldsymbol{x}}_{ic}(t) = v_{pi} \boldsymbol{u}_{ic}(t), \quad \boldsymbol{x}_{ic}(0) = \boldsymbol{x}^0_i, \\ \dot{\boldsymbol{x}}_{ec}(t) = v_{e} \boldsymbol{u}_{ec}(t), \quad \boldsymbol{x}_{ec}(0) = \boldsymbol{x}^0_e$$

$t \in [0, \bar{T}_f]$

$\boldsymbol{x}_{ic}(t) \in \mathbb{R}^2$：state position of $i^{th}$ pursuer $P_i$

$\boldsymbol{x}_{ec}(t) \in \mathbb{R}^2$：state position of evader $E$

$v_{pi}, v_c$：maximun speeds

$\boldsymbol{u}_{ic}(t), \boldsymbol{u}_{ec}(t) \in \mathbb{R}^2$：inputs，and $\mathcal{U} := {\boldsymbol{u} \in \mathbb{R}^2: ||\boldsymbol{u}|| = 1 \text{ or } \boldsymbol{u} = \boldsymbol{0}}$

• 每次输入的都是单位距离，只有游戏结束（捕获或者达到目标位置）的时候才输入$\boldsymbol{0}$

• 所以可以假设，所有参与者的控制输入，都是时间的分段常数函数

• 是每个单位时间间隔$[k\Delta t, (k + 1) \Delta t]$的输入，整个过程包含$\bar{K} + 1$个有限阶段，最多为$\bar{T}_f := \bar{K} \Delta t$

通过a simple forward Euler discretization scheme，得到如下的离散时间状态空间模型：

$$\dot{\boldsymbol{x}}_{id}(k + 1) = \boldsymbol{x}_{id}(k) + (v_{pi} \Delta t)\boldsymbol{u}_{id}(k), \quad \boldsymbol{x}_{id}(0) = \boldsymbol{x}^0_i, \\ \dot{\boldsymbol{x}}_{ed}(k + 1) = \boldsymbol{x}_{ed}(k) + (v_{e} \Delta t) \boldsymbol{u}_{ed}(k), \quad \boldsymbol{x}_{ed}(0) = \boldsymbol{x}^0_e$$

其中$\boldsymbol{u}_{ic}(\tau) = \boldsymbol{u}_{id}(k)$ for all $\tau \in [k \Delta t, (k + 1) \Delta t)$，and $\boldsymbol{x}_{id}(k) = \boldsymbol{x}_{id}(k\Delta t)$

2.3 Formulation of target-seekong evasion problem

• 前提假设：pursuer的首选策略是“relay pursuit”，相应的接力指标是“最短捕获时间”

即在每一时刻，主动追击者是pursuers中捕获时间最短的那个，同一时刻只有一名追击者处于主动状态，其他追击者处于静止状态

主动追击者的feed-back strategy为：

$$\boldsymbol{u}_{id}^*(\boldsymbol{x}_{ed}, \boldsymbol{x}_{id}) = \begin{cases} \boldsymbol{r}_{id} / ||\boldsymbol{r}_{id}||, \quad \text{if }i = i^*, \\ \quad \quad \boldsymbol{0} \quad \quad \text{ otherwise} \end{cases}$$

其中$\boldsymbol{r}_{id} := \boldsymbol{x}_{ed} - \boldsymbol{x}_{id}$是evader相对于$i^{th}$ pursuer的位置向量。

当捕获距离小于$l$或者目标距离小于$\epsilon$时，博弈中止

---

• 在本文中，假设所有的agents对其他agent的状态都是完全的，并且只有evader知道target的位置信息

3. Matrix game formulation of the multi-player PEG

在本文中，将$N+1$个agents的离散时间非零和博弈问题，重新描述为多行为两人零和矩阵博弈

考虑一个矩阵$M_k \in \mathbb{R}^{N \times (N + 1)}_{\ge 0}$

• entries为该阶段$E$的收益
• 每一行代表$P$采取的pure policy
• 每一列代表$E$采取的pure policy

在此处，$P,E$的控制输入空间（即决策空间）是连续的，包含无数个动作。对于$P$，仅考虑有限决策空间，仅仅包括能够增加收益的actions。$P$的$i^{th}$表示$i^{th}$作为主动追击者的策略。对于$E$，前$N$个动作依次对应于相应追击者的躲避策略，$N+1$为直接走向目标的动作。

• $(M_k)_{i,j}, i = j$：即为two-player zero-sum game的收益

• $(M_k)_{i,j}, i\ne j$：表示当$i^{th}$ pursuer为主动追击时，$E$试图躲避$j^{th}$ pursuer的动作

$E$并不知道$P$在当前节点的动作，所以有可能发生，并不是躲避主动追击者的情况

该矩阵必须在每个阶段都更新，也能反应博弈过程的潜在动态演化。该矩阵不同于重复静态博弈 的博弈。

3.1 Time metrics of the reach-avoid game

$$(v^2_e - v^2_{pi}) \phi^2 + 2(v_e \boldsymbol{u}_e^T\boldsymbol{r}_i - lv_{pi}) \phi + ||\boldsymbol{r}_i||^2 - l^2 = 0$$

所有的时间指标time metrics都与该方程的最小正解相关，该方程需要求解$\phi$

• $\phi_s(\boldsymbol{x}_e, \boldsymbol{x}_i, \boldsymbol{x}_T)$表示：

当evader直接前往目标位置时，第$i$个pursuer捕获evader的最短时间，此时该参数为上述方程在条件$\boldsymbol{u}_e = (\boldsymbol{x}_T - \boldsymbol{x}_e) / ||\boldsymbol{x}_T - \boldsymbol{x}_e||$下的解。

evader不会直接进行机动来躲避追捕者，只有追捕者会进行机动以最大限度缩短捕获时间，evader是通过控制与pursuer之间的距离，来延迟被捕获的

3.2 Elements of the payoff matrix

matrix每个元素都是一个数值，表示evader的双重目标：

1. 避免捕获
2. 到达目标位置

每个元素的两个组成部分：

1. $P$的捕获时间
2. $E$从当前位置朝向目标的程度

• $E$速度的目标朝向分量为$\cos{\theta}$，$\theta$是$\boldsymbol{u}_e$和$\boldsymbol{x}_T-\boldsymbol{x}_e$之间的角度

---

在每个阶段，至少有两个agent执行了动作，因此每个阶段结束之后需要重新构建matrix。

未来的收益与当前的收益同样重要，但是很难估计出evader在K个阶段之后的收益，因为每个阶段的收益取决于当前阶段的state。

当前阶段执行的action会反映在matrix的元素变化中，但是也不能够直接反映策略。

矩阵更新的伪代码如下：

Payoff Assignment to $M_k$
input: $x_e, x_T, x_i \forall i \in \mathcal{I}, k, \bar{T}_f$
output: $M_k$
for $i \leftarrow 1$ to $N$ do
for $j \leftarrow 1$ to $N$ do
$u_j = \frac{x_e - x_j}{		x_e - x_j		}$
$T_c = \min\{\phi_a(x_e, x_i, u_j), \bar{T}_f\}$
$G_c = \frac{}{		u_j				x_T - x_e		}$
$(M_1)_{i,j} = T_c$
$(M_2)_{i,j} = G_c$
end
end
for $j = N + 1$ do
$u_T = \frac{x_T - x_e}{		x_T - x_e		}$
for $i \leftarrow 1$ to $N$ do
$T_c = \min\{\phi_a(x_e, x_i, u_T), \bar{T_f} \}$
$G_c = 1$
$(M_1)_{i,j} = T_c$
$(M_2)_{i,j} = G_c$
end
end
$\hat{M}_1 = \frac{M_1}{\max_{i,j}(M_1)_{i,j}}$
$M_k = \hat{M}_1 + M_2$

• 主动追击者为i，evader躲避j，$T_c$为j在当前状态下追到e的最短时间/或博弈中止时间$T_f$

• $G_c$为j、e向量$u_j$，与e、T向量$u_T$之间的夹角

• $M_1 = T_c$，并normalize（j追到e的难度）

• $M_2 = G_c$，即夹角（或E朝向目标的程度）

3.3 Solution to the matrix game

将多人动态非零和博弈问题，简化为N+1个有限的两人零和多行为博弈问题，这个问题在混合策略中存在==鞍点解==

在阶段k，矩阵博弈的min-max solution由两个概率向量（离散概率分布）组成

1. For evader: $\pi_{ek}$
2. For pursuer: $\pi_{pk}$，用于整个追赶者群体

这两个向量对应于两个玩家的混合策略，混合策略向量的每个元素，对应于选择每个纯策略的概率

每个阶段k选择的离散动作，是混合策略分配的概率分布中的随机样本（？）

---

在每个阶段，只为agent选择一种纯策略，在极限情况下（对于无限阶段的游戏），选择纯策略的频率，收敛到混合策略$\pi_{pk}$和$\pi_{ek}$分配给纯策略的概率。

计算min-max问题中的鞍点向量$\pi^_{pk}$ and $\pi^_{ek}$，可以表述为==liner programming（LP）==，可以使用现成的求解器。具体来说，$\pi^{\star}_{pk}$对应于LP问题的解

4. New matrix formulation of the multi-agent PEG with Q-learning

本文中定义的new matrix为$M_k \in \mathbb{R}^{N_p \times N_e}_{\ge 0}$，其中$N_p, N_e$为P and E纯策略的数量，本文中定义的P处女恶略为2，E的纯策略为4

4.1 Discrete action sets for the players

该部分内容描述了定义的2种P and 4种E的纯策略

4.2 Q-learning for the matrix payoffs

通过Q-learning来获得matrix的每个元素

引入Q-learning之前必须定义新的状态空间（先前使用的位置向量，作为状态是不切实际的）

新的状态空间中的状态，是位置向量的的变换表示，并对追逃博弈的其他属性，进行编码

• 另外，通过捕获时间$\phi_c$和目标时间$\phi_T$的比值，可以准确反映博弈进程，并反映evader的安全性

4.3 Learning state space

5. Approximation of the payoff matrix with min-max Q-learning

• state transition function

$$\mathcal{T}_q: \mathbb{R}^m_{\ge 0} \times \mathcal{A}_e \times \mathcal{A}_p \to \mathbb{R}^m_{\ge 0}$$ $$\boldsymbol{\psi}(k + 1) = \mathcal{T}_q(\psi(k), p_i, e_j)$$

state transition是在position space中进行的，而不是在learning space当中，learning space是抽象化之后的特征空间，因此不适合用来做state transition

• reward function：$E$在每个state transition过程中的reward

$$\mathcal{R}_q: \mathbb{R}^m_{\ge 0} \times \mathcal{A}_p \times \mathcal{A}_e \to \mathbb{R}$$

• Heading function

$$\mathcal{H}_q: \mathbb{R}^m_{\ge 0} \times \mathcal{A}_e \times \mathbb{R}^2 \to [-1, 1]$$

该函数将状态$\boldsymbol{\psi}(k)$映射到evader的单位速度的参数$\vartheta$，通过将$E$的速度投影到目标向量$x_T$的视线上得到:

$$\mathcal{H}_q(\boldsymbol{\psi}(k), \boldsymbol{e}_j, \boldsymbol{x}_e, \boldsymbol{x}_T) := -\frac{\mathrm{d}}{\mathrm{d}t} \phi_T(\boldsymbol{x}_e(t); \boldsymbol{x}_T) \mid_{t=k\Delta t}$$

其中$\phi_T(\boldsymbol{x}_e(t); \boldsymbol{x}_T) := ||\boldsymbol{x}_t - \boldsymbol{x}_e(t)|| / v_e$

• Q-function

$$\mathcal{Q}: \mathbb{R}^m_{\ge 0} \times \mathcal{A}_p \times \mathcal{A}_e \to \mathbb{R}$$

Q-function将每一个tuple: (state, pursuer’s action, evader’s action)映射为$E$的reward

$$M_k(p_i, e_j) := \mathcal{Q}(\boldsymbol{\psi}(k), p_i, e_j; \boldsymbol{x}_e, \boldsymbol{x}_1, \dots, \boldsymbol{x}_N, \boldsymbol{x}_T)$$

5.1 Linear approximation of the Q-function

$$\mathcal{Q}(\boldsymbol{\psi}(k), p_j, e_j) = \boldsymbol{w}^T_q \zeta(\boldsymbol{\psi}(k), p_j, e_j; \boldsymbol{x}_T)$$

其中：

$$\zeta(\boldsymbol{\psi}(k), p_j, e_j; \boldsymbol{x}_T) := \left[ \begin{matrix} \mathcal{H}_q(\boldsymbol{\psi}(k), \boldsymbol{e}_j, \boldsymbol{x}_e, \boldsymbol{x}_T) \\ (\mathcal{T}_q(\psi(k), p_i, e_j))_1 \\ (\mathcal{T}_q(\psi(k), p_i, e_j))_2 \\ (\mathcal{T}_q(\psi(k), p_i, e_j))_3 \end{matrix} \right]$$

并且：

$$\mathcal{Q}(\boldsymbol{\psi}(k), p_i, e_j; \boldsymbol{x}_e, \boldsymbol{x}_T) = \mathcal{R}_q(\boldsymbol{\psi}(k), p_i, e_j; \boldsymbol{x}_e, \boldsymbol{x}_T) + \gamma \min_{i^{\prime}}M_{k + 1} \boldsymbol{\pi}_{e_{k+1}}$$

5.2 Reward function

奖励函数由三部分组成

• target-heading reward

$$\mathcal{H}_q(\boldsymbol{\psi}(k), e_j, \boldsymbol{x}_e, \boldsymbol{x}_T) := -\frac{\mathrm{d}}{\mathrm{d}t} \phi_T(\boldsymbol{x}_e(t); \boldsymbol{x}_T) \mid_{t=k\Delta t}$$

• state-transition reward

$$\mathcal{R}_s(\boldsymbol{\psi}(k), \mathcal{T}_q(\boldsymbol{\psi}(k), p_i, e_j)) := (\mathcal{T}_q(\boldsymbol{\psi}(k), p_i, e_j))_3 - (\psi(k))_3$$

相较于目标时间，文中积极奖励捕获时间

• terminal reward

$$g(\boldsymbol{\psi}, e_j) := \begin{cases} +1, \quad & \text{if } \psi_4 = 0, \\ -1, \quad & \text{if } \psi_1 = \psi_2 = \psi_3 = 0, \\ 0, \quad & \text{otherwise} \end{cases}$$

• total reward

$$\mathcal{R}_q(\boldsymbol{\psi}(k), p_i, e_j; \boldsymbol{x}_e, \boldsymbol{x}_T) = \mathcal{H}_q(\boldsymbol{\psi}(k), e_j, \boldsymbol{x}_e, \boldsymbol{x}_T) + \mathcal{R}_s(\boldsymbol{\psi}(k), \mathcal{T}_q(\boldsymbol{\psi}(k), p_i, e_j)) + g(\boldsymbol{\psi}, e_j)$$

在训练过程中，最重要的是，使训练奖励尽可能独立于timestep、specific value。本文中考虑了奖励第一项（target-heading reward）的采样周期限制

6. Numerical simulations

• 讨论了两种类别的evader

  1. 速度比pursuer慢
  2. 速度与pursuer相同

• 性能对比：Q-learning and without any learning

• 测试过程中：pursuer数量、网格大小与训练过程不同

值得注意的是，本文设计的Q-learning的matrix大小，与pursuer的数量无关，取决于定义的new matrix

数值仿真的结果显示，使用Q-learning的方法，有更高的效率，以及能够生成非学习方法生成不了的策略

7. Summary

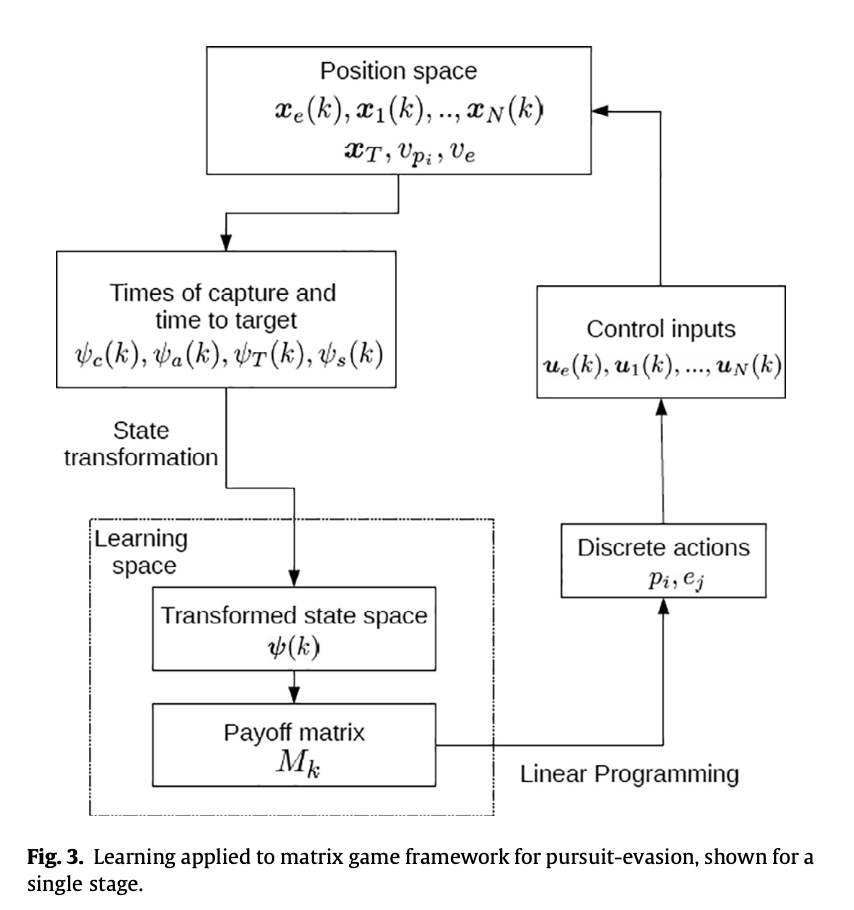
本文的框架入上图所示，主要工作及创新点在于：

• Position space：问题建模
• Times of capture and time to target：参数建模
• State transformation：创新点1
• Transformed state space：创新点2
• Payoff matrix：创新点3，new matrix与参与者的数量无关
• Linear Programming && Discrete actions：
• Control inputs

从算法上来说，并没有很难的地方，主要创新在于new matrix